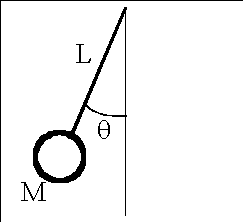
1. Introduction

This problem builds upon the two previous spreadsheets, and introduces a problem that is often discussed in physics textbooks, but rarely solved explicitly

.

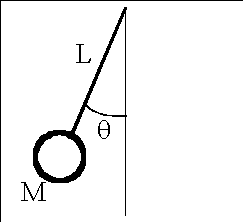
The problem is to determine the motion of a simple pendulum, oscillating in a plane under the influence of gravity. The pendulum is a mass M at the end of a very light rigid rod of length L. Since the mass is confined to a plane at the end of a fixed-length rod, this is a one-dimensional problem in terms of an angle q. Let q=0 when the rod is hanging vertically downward. The motion of the mass is defined by the equations:

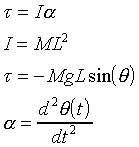[1]

These equations are the torque equation, definition of moment of inertia, definition of torque, and definition of angular acceleration, respectively.

Combining these expressions, you can get the equation of motion for the angle q, as

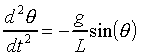. [2]

For very small q, sin(q)»q, and the simple-harmonic oscillator formula results:

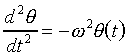, [3]

where w²=g/L, which has the solution

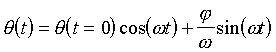, [4]

where we have defined the initial angular position q(t=0)=q₀, and the initial angular velocity f = dq/dt at time t=0.

This is all straightforward. When the initial angle is not small, or the initial angular velocity is not small, this problem does not have a simple analytical solution. However, your spreadsheet skills can be used to solve the problem by integration of the equation of motion. This requires two steps. You start with a given angle and angular velocity (the initial conditions). From these, you calculate a new position from the velocity, and a new velocity from the acceleration:

Euler Method:

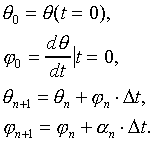[5]

Half-Step Method:

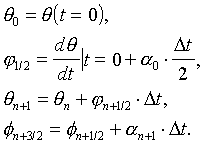[6]

In all of this, the angular acceleration is given by

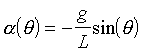. [7]

With these simple expressions, you have solved a second-order differential equation by two steps of numerical integration.

2. Tasks

Let the length of the rod be L= 10 meters. Determine a small step size in time Dt, and a number of steps N, so that you calculate the angle q(t) for 2 complete oscillations for the limiting case of when q(t=0) is small (less than about 15 degrees).

1. Calculate the ``natural frequency'' of the oscillation of this pendulum in the small-angle limit, for zero initial angular velocity. Do this once using the Euler method, and plot a graph. Then do it again with the half-step method, and plot a graph. Note that the half-step method works much better than the Euler method. Use the half-step for the rest of this problem.
2. Calculate the period of oscillation T as a function of initial angle q, for zero initial angular velocity. Plot your result. What is the effect of the sin(q) dependence of the force on a simple pendulum?
3. Plot the ``phase plane'' for the pendulum. This is the graph of the angular velocity as a function of angular position. Do this for a number of starting angles, with zero initial velocity.

EXTRA CREDIT: If you start the pendulum at the top with some additional velocity, it will have a very different behavior in the ``phase plane'', since it will no longer have a simple oscillatory behavior.

EXTRA CREDIT: Put in some friction in the pendulum bearing. The friction force is a torque that acts in the direction opposite to the angular velocity (f) of the pendulum. You can write this as

,

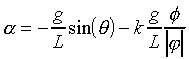where the angular velocity is f=dq/dt, and k is the coefficient of friction (you could use k=0.1).