This problem introduces the use of Euler's method for computing the equation of motion of a classical particle in two-dimensions, with time as a parameter. We've already done this for one dimension, so it is just a simple extension to motion in a plane. This is just the "cannon-ball" problem from first-year physics. The difference is that we can do the problem correctly.
It also introduces the use of the Data Table (What If?) tool of the spreadsheet, which effectively treats the spreadsheet as a large 'black-box' function.
The problem is to determine the motion of a particle in a vertical plane, subject to air resistance (drag). The motion is assumed to be in the x-y plane. The particle starts out with some initial velocity, and then moves under the influence of gravity (which is an acceleration in the -y direction), and drag. Drag always acts in a direction opposite to the instantaneous velocity.
The equation of motion is given by
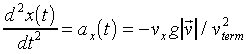 [1]
[1]
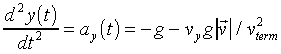 [2]
[2]
in the y-direction.
The amount of drag is specified by the terminal velocity,
vterm2. This is the velocity that a particle
would achieve if dropped (from an infinite height) with zero initial
velocity, and allowed to fall under the influence of gravity and
drag. The drag builds up until the total acceleration (gravity
plus drag) is zero, and the velocity becomes a constant (its "terminal"
value).
Solve the equation of motion using the Euler method. This is valid
because you have an explicit equation for the acceleration in
terms of the velocity.
Euler's method in this case can be written:
where the acceleration is computed using the formulae above, [1]
and [2]. You start out your values by specifying initial x and
y positions, and initial velocities in the x and y directions.
Create a spreadsheet to calculate the x(t) and y(t) positions
of the particle as a function of small time steps. Create a data-table
to use the spreadsheet to calculate the range or maximum
x-distance as a function of initial conditions, and the time
of flight. Use an initial velocity of 45 m/s.
1. Trajectory plots: Calculate and graph y(t) vs x(t) for
very small drag, intermediate drag, and high drag. Note that high
drag has a low terminal velocity. Assume the initial angle is
45 degrees.
2. Range plots: Calculate and graph the range as a function
of initial angle, for low, intermediate, and high drag.
3 [EXTRA CREDIT]. Time-of-flight plots: Calculate and graph
the time-of-flight as a function of initial angle, for low, intermediate,
and high drag.