You should re-acquaint yourself with the relationships between charge density, electric potential, and electric fields. We will use partial-derivatives of functions of two variables to derive the equations for the spread-sheet, but you will only need the results to work the problems.
So far, we have been using the spreadsheet capabilities as a kind of very sophisticated programmable calculator. In this assignment, we will use the spreadsheet in a different way. The problem is to simulate the electric potentials that are created by metal electrodes of various shapes, biased to fixed voltages. Such electrodes are found in a variety of devices, such as vacuum tubes, CRT screens, electron lenses, and semiconductor devices.
The simulation uses the spreadsheet 'cell' to represent a physical location in a two-dimensional (x,y) space. The cell contains a formula, and the formula evaluates the potential at the location in space represented by the cell.
The technique we will use is called the Finite-difference Method. It is one of the two most common ways of solving complex simulation problems which are based on the solution of a partial differential equation (the other method is closely related and is called the Finite-element Method). Many practical problems are characterized by a partial differential equation. Electric and magnetic fields created by electrodes and currents are one type of problem. Another is the stress and bending of structural members (steel beams, concrete pillors, etc.) in buildings or bridges. Still another is the problem of fluid flow around objects (aircraft, submarines).
The equation that determines how the electric potential varies in space is called Laplace's equation. In our problem, there will be no free charges, only empty space and metal electrodes held at specific constant voltages. In addition, we will assume that the problem can be accurately modelled in only two dimensions, so that the potential is V=V(x,y) . With these simplifications, Laplace's equation is
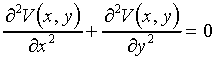 . [1]
. [1]We still need to turn Laplace's equation into a formula that can be used in a spreadsheet. I'm going to show you how to do this, but you should know that the answer is so very simple that you can skip to the end and get started with your spreadsheet if you like, and come back to the derivation at your leisure.
First, I will need to introduce some shorthand notation to make it easier to write things down. We are going to expand the potential V(x,y) in a Taylor series around the point x0,y0 . Let the potential at this point be V(x0,y0)=V0 . I also need the value of the derivatives of the potential, evaluated at the point x0,y0 . Let me write them in the following ways:
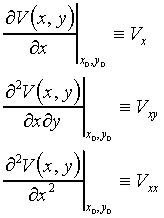 [2]
[2]Note that the various derivatives, Vxx, Vyy , etc. are evaluated at the point (x0,y0) , and are therefore just numbers (constants).
We can then expand the potential in a series in x and y around the point (x0,y0) :
The trick is to evaluate the potential at four neighboring points, above, below and to the side of the point (x0,y0) . These points are at (x,y) = (xo±d,yo±d) . Lets call these points North, South, East and West. The potential at the four neighboring points is given by
VS = Vo - Vx d+ 1/2 Vxx d2
VE = Vo + Vy d+ 1/2 Vyy d2
VW = Vo - Vy d+ 1/2 Vyy d2 . [4]
We therefore have the very simple result for a 'law' governing the potential in two dimensions: the value of the potential at any point is just the average of the potential at the four nearest-neighbor points:
You will be designing some electrode configurations, and using the finite-element technique to determine the potential. From the potential you will be able to get the electric field. The potential is a scalar quantity (just a number), but the electric field is a vector (it has a direction in the x-y plane). The value of the electric field in the x and y directions can be determined from the derivative of the potential, using the spreadsheet approximation for the derivative:
Ey (x,y) = -[V(x,y+d) - V(x,y)]/d . [6]
Use units of Volts for your potential, and meters for the distances.
- Calculate the potential for a "short" parallel-plate
capacitor. This is a pair of thin plates whose length L is close
to the spacing D. Let the plates be parallel to the x-axis. The
potential on one plate is V=0, and V=1 on the other plate. Plot
the potential along the y-axis in the middle of the capacitor
and at the end. Plot the electric field in the x and y directions
at the middle of the capacitor and at the end.
- Repeat the capacitor design problem for a "long"
capacitor. You should let L be sufficiently larger than the spacing
D so that you see a difference in the behaviour of the capacitor,
as compared to the L=D case.
EXTRA CREDIT SELECTIONS:
- An electron lens can be constructed from three thin parallel plates, oriented parallel to the x-axis. The spacing between the plates is D, and the length should be at least a few times larger than D. Put a hole in the central plate, of size A=D/2. The outside plates are at V=0, the central plate is at V=1. Calculate the potential along the y-axis, from one end of the lens to the other, going through the center of the hole. Do the same for a line that passes by the edge of the hole. Plot the electric field in the x and y directions, along the axis that goes through the center of the hole.
- STM microscope tip: Model the tip of a scanning tunneling microscope by having a sample at zero potential (a thin plate parallel to the x-axis), and a sharp tip at V=1 near the surface of the sample. The distance between the sample and the end of the tip is about 10-9 meters. The tip can be modelled as a triangle with an apex angle of 45 degrees or so.
- Try your own arrangement of electrodes.